One More and Place Value – Our Base Ten System

Within our number system the concept that adding one more unit makes the next named number is the first and most prominant learning. Young children who learn to count may not be able to say the value of a number if one more is added. When asked to follow a practical demonstration, e.g. you have six buttons (presented on the table) and then I give you one more button (one button is added to the group of six) now how many buttons do you have?; young children usually have to recount the buttons to reach the answer seven. Similarly young children who can count confidently may not have an understanding of the conservation of number. This child has to recount the same objects when they are moved into a different pattern, or a different place or they just look different because something else has change. For this child adding one more is a new counting task rather than an auditory request for what number comes next. Older children who are working with number sums between 1 and 50 and can identify and count up to 100 and more, often cannot answer the questions of one more such as 44+1= ?  or 89+1= ? If a person has secured this one more aspect of our numerical counting structure then any question even those with very high numbers such as – a million and four add one, and fifteen thousand six hundred and eighty three add one, will be answered immediately [providing they can correctly recall the original number that was said]. This is a good memory game to play and if participants are also asked to record the question as a sum, they can get good practice transcribing large numbers from their spoken form into their visual (written) numerical formate. Games related to the process of adding or subtractingone can be explored throughout a person’s life of learning about numbers.

The use of any form of counting frame is based on this concept of one more. The standard base ten abacus illustrates the more complex aspects of place value however the abacus can be used successfully even without any numerical understanding if the process of adding one more is maintained accurately when moving the beads on the abacus.

In our base ten system of counting, ten is of critical importance. This is illustrated by the traditional abacus which only has nine counters on each row. Now the 0 still means nothing but it is also used to create a new concept that of place value. The 1 when written as part of a ten means one group of ten, thus the value of each numerical symbol must now also be related to the concept of place value.

An outdoor version of the above exploration of numbers up to 15 or twenty is as follows. Make a collection of something that is easy to find lots of the same, such as sticks, stones of a similar size, wild flowers e.g. daisies, acorns, conkers. Use this collection to build a number stair as above. The blocks of ten could be presented in on small plates or in individual baskets or paper bags. For example: Collect twelve twigs. Select two (or make two or find two) twigs that look the same and, name these the two twins and separate them from the other twigs. Count the remaining twigs then put all ten of them into a paper bag. Now the explorer has 1 bag of ten twigs and the two twins, one bag of ten and two more makes twelve. The 12 sticks could be accompanied by a written sum 10 + 2 = 12 and/or the spoken/written sentence ‘one ten and the two twins made twelve twigs.’ Working outside in natural environments support understanding and confidence in number conservation, and encourages number activities that extend auditory counting and visual organisation  related to how the numbers are presented verbally and numerically.

‘Shut the Box’ A Number Bond Game.

Materials: Each player has:- a ten space egg box and a set of numbers 1 to 10. Each player places their numbers in the egg in numerical order as shown. Players then take turns to shake a ten sided dice numbered 0 to 9. (if a dice is numbered 1 through to 10 then the one on the ten number on the dice will need to be removed or whited out to give numbers 0 to 9). Each player shakes the dice and then collects, if required, the number presented on the dice and places it into the space that completes the sum of the two numbers to give a total of ten.

Alternatively one set of cards (or tiles) numbered 0 to 9 is collected for each player into a combined pack of cards. For example if there are three players the shuffled set of cards would amount to thirty cards (three of each number nought to nine). These cards are then placed in rows face down on the table. Each player then takes his turn to turn over one of the cards and places it in into the appropriate egg space in his box – so that the sum of the two numbers equals ten. If a player does not need the card he turns over then the card is left in its place face down. This enables other players to remember where the card is on the table in case it is needed for his own egg box. The first player to complete all ten egg spaces with number bonds to ten then shouts “Shuts the box!” and completes his round by counting in tens to 100 as shown on the lid of the box. The game can continue with the other players until everyone has a shut box.

The author has used beads threaded into lengths of one through to ten, so that each player places the correct string of beads into each egg space in the open box and then the players take it in turners to collect another string of beads from a bag. Thus the players now have to use touch if they wish to locate a specific number bead length because they cannot see inside the when it is their turn to retrieve a length of beads. Another way to add a kinaesthetic element to the game can be achieved by painting the numbers onto glass buttons or small tiles (2cmsquared) sold at the local DIY store.

The Eastwood Odd and Even Bricks

Once the counting of numbers gets beyond the units and into tens a new concept and structure of information becomes essential to any practical number activity – that of number bonds for ten. The following game was designed by the author to encourage and consolidate this foundation of number bonds that is essential for all numerical operations and further understanding of numeracy.

This activity can be done by an individual or played as a game with two or more players taking turns. The aim is simply to build the blocks into groups of ten.

Firstly the blocks are presented in numerical order.

Using two or more sets of the above bricks and a corresponding set of numbered cards that can initially be matched to the number blocks before being shuffled and place face down. The player/s turn a card over when it is their turn to build a set of ten. The card taken from the stack is placed on the first box then the player collects the appropriate block of bricks and places them on their sum card in the first box (as shown below). The player then places the appropriate number block in the second box and the blocks are placed together over the drawn 10 block shown after the equals sign. A set of sum cards are also available to be matched with each conclusion.

A Number Bond Number Rhyme

One and nine, socks on the line.
Two and eight, children on the gate.
Three and seven, might get us to Devon.
Four and six, get some pick and mix.
Five and five, bees in the hive.
Six and four, please close the door.
Seven and three, now let’s get some tea.
Eight and two, I’m ok and so are you.
Nine and one, our rhyme is done.

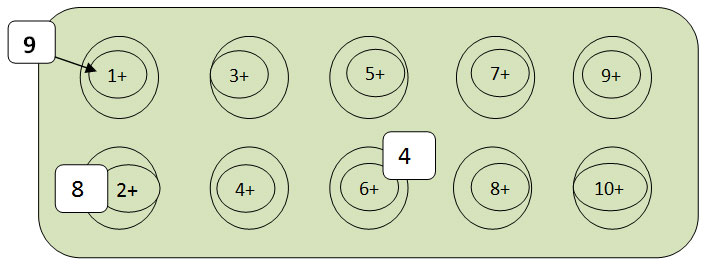
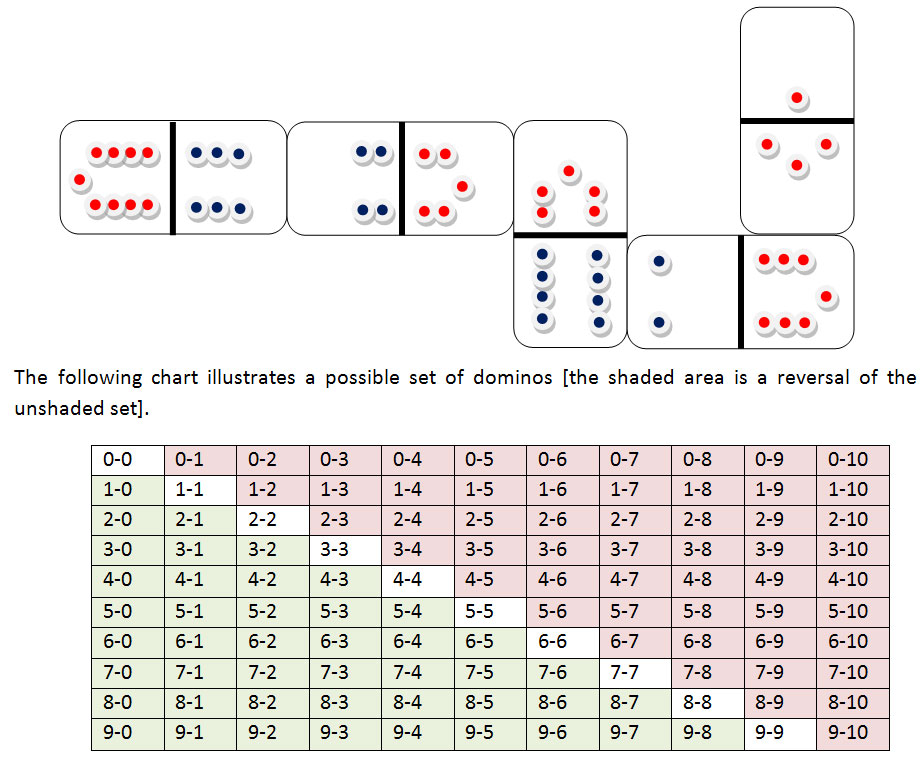
Number Bond Dominoes

One can make a domino game for number bonds 1-9 or 0-10. In this game the dominoes can be placed if the two adjacent numbers make 10. The author likes to make these dominos with a strong visual design that encourages to group the numbers into the value of 10. Also the odd and even numbers can be presented in different colours. The coloured patterns of dots are placed against the centre line of each domino.

The use of written numbers would could create and encourage a disregard for the correct orientation of the number symbols [especially 6 & 9]. This confusion would be created by different players viewing and placing the numbers from an extensive variety of different directions.

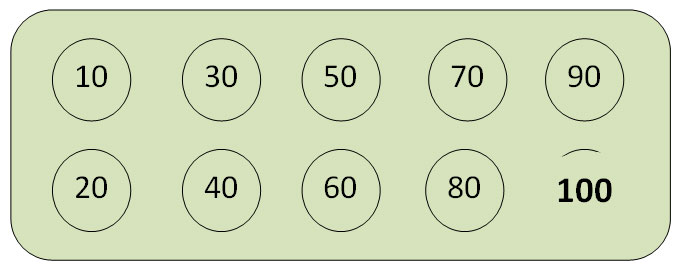
The Eastwood Bingo Game

The Author has created the following special Bingo games that also encourage a knowledge of numbers beyond 10 and up to 100.
These games have many variations and can be graded to suit the participants’ age, ability, enthusiasm and sustainable focus.
The bingo cards are simply empty squares structured in rows of ten.]These cards are of three sizes – two rows of ten equalling twenty or five rows representing one to fifty and ten rows, one to one hundred. All the players have the same size bingo card and the caller only presents numbers within the range of squares presented on the cards.[A simpler and shorter version of the game is when each bingo card has a different set of correctly numbered boxes. These numbered boxes present a bonus of squares that do not need to be called and covered during the bingo game. Thus, each player has the potential to cover all their boxes with a counter before any other player.]
The caller shuffles a set of number cards and then turning them over one at a time, gets a random order for the number range presented on the bingo cards. The caller can present these numbers one at a time in using one or more of the following methods of illustration:-
Spoken verbal identification, i.e. when the caller says nine the bingo players find the ninth square on their card and place a counter in the square to show that it has been called. For example, the Bingo card below says that 20,   13,   14  and 9 have already been called and the numbers 6, 11,and 16 are given as a free start.

Alternative ways that the caller can present numbers are as follows:-

• As standard written numbers 10, 15 etc.
• As tens and unit cards. 
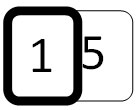
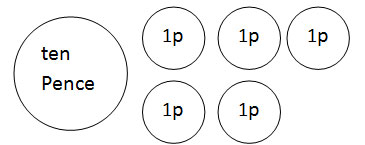
• As money 
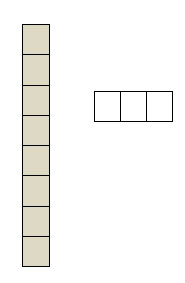
• As tens and unit blocks:- 
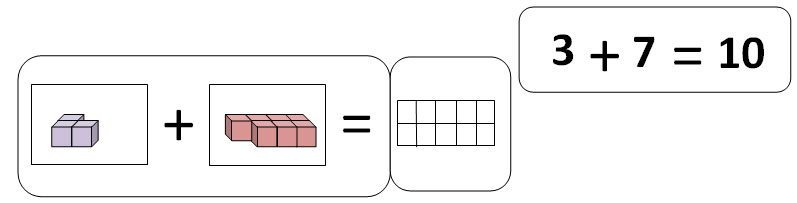
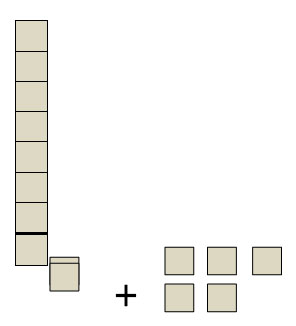
• As a visual sum 
• As a spoken quiz question – “What number comes before 16”….or “If you had seven apples and john had eight how many have you got altogether.
• As a spoken and/or written sum 3×5 or 12+3

Understanding the base ten system

The base ten system of place value is fundamental to all aspects of numerical calculation. The most effective multisensory representation of the base ten from 1 to 1000 is presented by the three dimensional blocks. Whereby one centimetre cube represents one unit, a ten by one centimetre rod presents ten, a ten by ten one hundred square presents a hundred cubic centimetres and the ten by ten by ten solid cube presents one thousand cubic centimetres. Using these blocks numbers can be felt as size and weight, counted, and structurally built. Using the blocks to build creative structures can be followed by an accurate assessment of the number of centimetre cubes that have been used in any specific structure. When the structure is dismantled the number of bricks used can be illustrated by reorganising the blocks into physical groups of units tens hundreds and thousands respectively.

A similar game can be played with money (real or imitation). The money is placed into a small container e.g. a clear jar or a small box. Participants then guess the total value of the money in the container. Then the money is physically grouped into 10 pounds, pounds, ten pence, and odd pence to illustrate and prove the correct amount of money placed in the jar or box.

Another popular version of this counting activity is to fill a decorative jar with coloured glass pebbles (those sold as an indoor decoration for plant pots). Then friends and family are asked to guess the total number of glass pebbles in the chosen container. Then, using one or more appropriately sized 100 square grids, the glass pebbles are placed one on each square so that the correct total number can be clearly identified

The Eastwood Symbol Maths  [The Eastwood Symbol Maths is presented in full in the Numeracy section Folder 3: Files 4^th(3d);  4^th(3e)  &  4^th(3f) ]

Symbol maths is used by the author to bridge the transition from three dimensional concrete number activities onto formal written numerical calculations, i.e. sums.

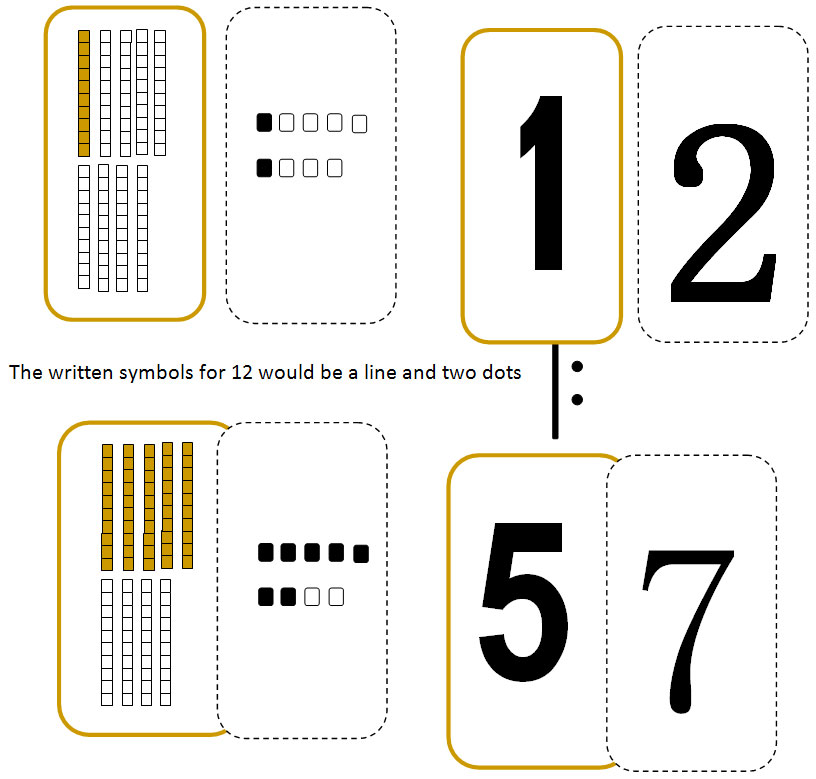
The written symbols for 57 would be five lines and seven dots:-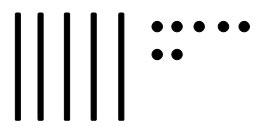 

The written symbols for 146 would be a square, four lines and six dots.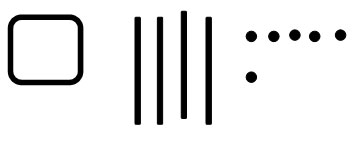 

The written symbol for 1000 is a square (as used for the one hundred) with a cross inside to represent the 3D thousand centimetre cube that represents 1000 in the base ten block set. 

The Wonders of the traditional Abacus

In Japan children from three years onwards learn to use an abacus. This system of teaching and performing basic arithmetic operations offers a kinaesthetic understanding of the base ten system of numeracy that is also illustrated as a visual representation of numerical operations and the resulting answers. This visual presentation is later the numbers and . When the children are older they can do complex calculations without an imaginary abacus, thus rapid finger movements are associated with internalised visual imagery that ultimately presents the answer as it would be seen on an abacus.   Tables below present the base ten numbers in relation to the different value of one in the different columns indicated by the number of noughts between the one and the decimal point.

[From right to left each column represents 10 x bigger]

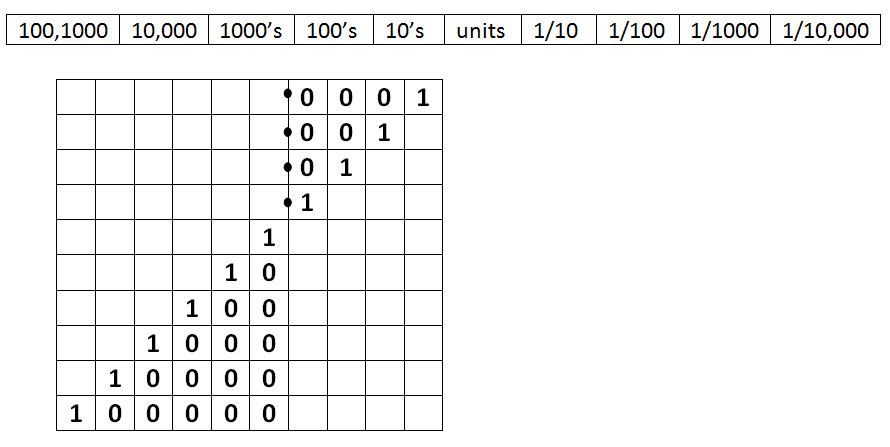
The tables above illustrate the regular structure of our number base system and encourage those with a good understanding of our number system to clarify the simplicity and repetitive nature of the base 10 numerical structure. Those without extensive experienced and understanding, the charts above may have little or no useful meaning. However, the young children in Japan, using an abacus gain a kinaesthetic understanding of base-ten numeracy. Those who attain high levels of efficiency with the use of an abacus for complex mathematical operations can ultimately work without physically using an abacus. instead they move the fingers over an imaginary abacus and their imagination and the integration of kinaesthetic movements with visual memory enables the person to very quickly calculate correct answers, to visual as well as auditory mathematical calculations using any combination of the four operations, addition, subtraction, multiplication and division.